CIE Extended Mathematics (2017-18) Algebra2

Algebra2 (2017-2018)

Click Here for Short Answer

11	$( 2018/$s$/21/$img$/$q$21) $ There are four inequalities that define the region R. One of these is $y\leqslant x+1.$ Find the other three inequalities. [4]
12	$( 2018/$s$/22/$img$/$q$19) $ Find the two inequalities that define the region on the grid that is not shaded. [3]
13	$( 2018/$w$/22/$img$/$q$14) $ By shading the unwanted regions of the grid, find and label the region $R$ that satisfies the following four inequalities. $$ x\leqslant3\quad x\geqslant2\quad y\leqslant2x+1\quad y\geqslant4-x $$ [3]
14	$( 2017/$s$/23/$img$/$q$11) $ By shading the unwanted regions of the grid above, find and label the region $R$ that satisfies the following four inequalities. $$ x\geqslant0\quad x+y\geqslant7\quad y\geqslant x\quad x+2y\leqslant20 $$ [3]
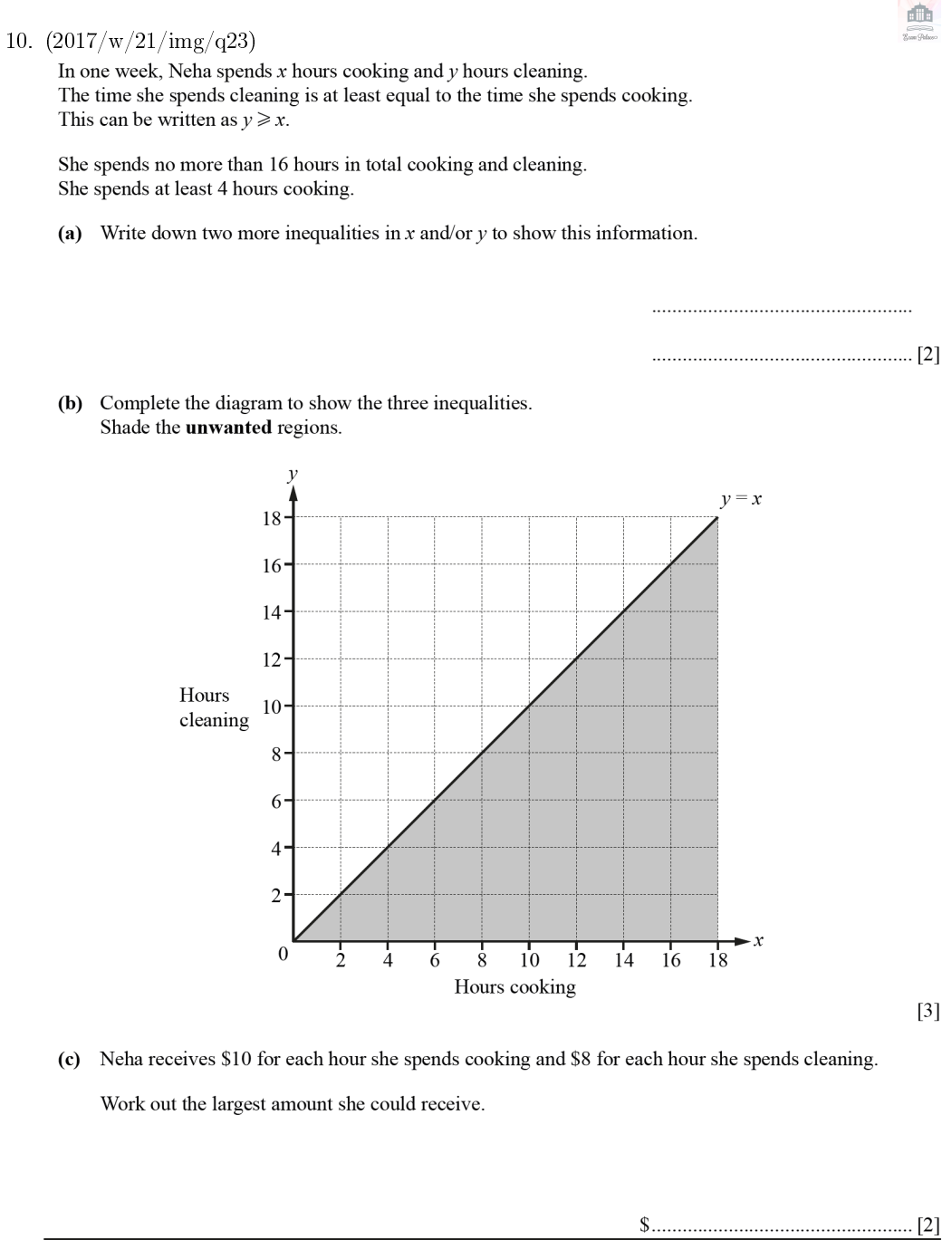
15	$( 2017/\mathrm{m/42/img/q9a) }$ Bernie buys $x$ packets of seeds and $\gamma$ plants for his garden. He wants to buy more packets of seeds than plants. The inequality $x>y$ shows this information. He also wants to buy $\begin{array}{l}\\\bullet&\text{less than 10 packets of seeds}\\\bullet&\text{at least 2 plants.}\\\end{array}$ (a) Write down two more inequalities in $x$ or $\gamma$ to show this information. $\cdot[2]$ (b) Each packet of seeds costs Șl and each plant costs $\$3$. The maximum amount Bernie can spend is $\$21$. Write down another inequality in $x$ and $y$ to show this information.[1] (c) The line $x=y$ is drawn on the grid. Draw three more lines to show your inequalities and shade the unwanted regions. [5] (d) Bernie buys 8 packets of seeds. (i) Find the maximum number of plants he can buy.[1] (ii) Find the total cost of these packets of seeds and plants[1]
16	$( 2018/$m/42/img/q6a$) $ Klaus buys $x$ silver balloons and $y$ gold balloons for a party. He buys $\begin{array}{lll}\bullet&\text{more gold balloons than silver balloons}\\\bullet&\text{at least 15 silver balloons}\\\bullet&\text{less than 50 gold balloons}\\\bullet&\text{a total of no more than 70 balloons}\end{array}$ (a) Write down four inequalities, in terms of $x$ and/or $y$, to show this information.[4] (b) On the grid, show the information from part(a) by drawing four straight lines and shading the unwanted regions. (c) Silver balloons cost $\$2$ and gold balloons cost $\$3$. Calculate the most that Klaus could spend.[2]
17	$( 2018/$s/43/img/q9$) $ (a) Find the equation of the straight line that is perpendicular to the line $y=\frac{1}{2}x+1$ and passes through the point (1,3).[3] (b) (i) Find the three inequalities that define the region $R.$ [4] (ii) Find the point (x,y), with integer co-ordinates, inside the region $R$ such that $3x+5y=35.$ [2]