TOK (Theory of Knowledge) Mensuration

 Mensuration

In this Chapter, we are going to recap the basic knowledge regarding “Mensuration". The following descriptions are summarized for preparation of past paper practice and if you do not know something, you can contact us.

Area

• Rectangle - $l \times b$, where l=length, b=breath

• Trapezium - $\frac 12 (a+b)h$, where a=length of one parallel side, b= length of the other parallel side, h= height between parallel sides.

• Kite - $\frac 12 a \times b$, where a and b are diagonals.

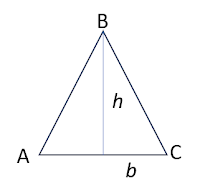
• Triangle - $\frac 12 \times bh$, $\frac 12 ab \times sin\angle C$

 

The Circle

• Circumference = $\pi d$= $2\pi r$, where d= diameter, r= radius, $\pi$=3.142….
• Area = $\pi r^2$

 Arc Length and sector area

• $A= \frac {\theta}{360}\times \pi r^2$
•  $l=\frac{\theta}{360} \times 2 \pi r$ , where l=arc length

Chord of a circle

 

Chord = AB

The Shaded Region =  minor Segment

The unshaded Region (whole circle except minor segment) = major segment

In $\odot O$, If OC $\perp$ AB, then C is the mid point of AB and vice versa.

Area of Minor segment = Area of sector – Area of Triangle

 

 

Volume

Prism- $A \times l$, where A= area of cross section , l = length

Cuboid – a prism with six faces being rectangles

Cube – a prism with six faces being squares

 Cylinder - $\pi r^2 h$, where r= radius, h= length

 

Pyramid - $\frac 13 $ (base area) $\times $ height

Cone - $\frac 13 \pi r^2h$

Sphere - $\frac 43 \pi r^3$

Surface area

 

• Cylinder - $2 \pi rh$
• Sphere - $4 \pi r^2$
• Cone - $\pi rl$, where l = slant height

 

Congratulations! You are ready to practice past papers. you can click Home button and choose the post you would like to practice. See you in the next chapter